plotting masters - a professional guide - Teil I
Grafische Interpolation und Bestapproximation von numerischen Wertepaaren: Wir wollen Punkte auf einer Zeichenebene über verschiedene Verfahren miteinander verbinden.
2015-01-25 15:16:30 2022-12-05 12:17:44 EVAMasters
Berlin Jun 09
Mit dem Erscheinen der Beta-Version wurden die «prototypischen Schlampereien» bei der Rechnung mit Gleitkommazahlen durch geeignete Rundungstechniken besser konditioniert.
Informelle Spezifikation
-
Es ist nach einem kleinen aber flexiblem PHP-Programm zum Zeichnen von kartesischen Diagrammen gesucht. Wir folgen dabei einer intuitiven Vorgehensweise: Eine Zeichenebene dient als Container für unterschiedliche Diagrammtypen, so z.B. Linien-, Punkt- oder Kurvendiagramme. Jeder derartigen Komponente werden numerische Wertepaare übergeben, die dann über die jeweiligen Verfahren interpoliert oder approximiert werden. Wir wollen hier eine stückweise lineare Interpolation (Polygonzug), sowie eine natürliche Spline-Interpolation von Wertepaaren realisieren. Wir werden auch sehen, wie sich sogar Balkendiagramme mit diesem Kontext vertragen können.
Motivation
-
Das folgende Programm zeigt, wie mit PHP die obige Anforderung umgesetzt werden kann. Der Programmumfang umfasst keine 1000 Zeilen. Somit ist der geübte Programmierer in der Lage, das Programm an die jeweiligen Bedürfnisse anzupassen.
Ausblick
-
Neben den hier vorgestellten Interpolationsverfahren spielt ebenso die Ausgleichsrechnung (Bestapproximation) eine praktische Rolle, deren Graphen im Unterschied dazu nicht zwangsläufig durch alle Wertepaare hindurchgehen. Vielmehr ist man an einer bestmöglichen (gewichteten) Annäherung durch einen Graphen mit vorgegebenen Eigenschaften interessiert. Je nach freien Kapazitäten komme ich darauf zurück.
Beispiel 1 (Interpolation von numerischen Wertepaaren)
-
Zu Beginn jeder grafischen Visualisierung von Wertepaaren initialisiert man stets ein Exemplar vom Typ Graph - unsere Zeichenebene. Diese Instanz nimmt anschließend mittels Add die verschiedene Komponenten vom Typ GraphComponent auf. Der Zeichenvorgang berechnet aus allen Komponenten die jeweilige Skalierung für jede einzelne Komponente, so dass alle Komponenten in der Zeichenebene Platz finden und damit vollständig sichtbar sind. Der Konstruktor von Graph hat kein Argument.
1
2 $g = new Graph();
3
Wir wollen folgend drei Komponenten mit gleichen Wertepaaren grafisch visualisieren, um die spezifischen Unterschiede zu demonstrieren. Die jeweiligen Konstruktoren der einzelnen Komponenten nehmen einen hexadezimalcodierten RGB-Farbwert entgegen, in der die Komponente gezeichnet werden soll. Die Komponente c1 soll unsere Wertepaare durch Punkte interpolieren, d.h. die Punkte als schwarze «kleine Quadrate» zeichnen.
1
2 $c1 = new GraphPoints(0x000000);
3
Die Komponente c2 soll unsere Wertepaare als stückweise lineare Interpolierende darstellen, d.h. alle Punkte über eine blaue Linie verbinden.
1
2 $c2 = new GraphLinear(0x0000FF);
3
Die Komponente c3 soll schließlich unsere Wertepaare als natürliche Spline-Interpolierende darstellen, d.h. die Punkte werden über eine rote Kurve verbunden.
1
2 $c3 = new GraphNaturalSpline(0xFF0000);
3
Die Komponenten müssen nun an die obige Zeichenebene $g gebunden werden. Unser «Container» wird also über alle Komponenten, die wir zeichnen wollen, «informiert». Die Bindereihenfolge bestimmt dabei die Sichtbarkeit, d.h. die zuletzt eingefügte Komponente überdeckt stets ihre Vorgänger.
1
2 $g->AddComponent($c1);
3 $g->AddComponent($c2);
4 $g->AddComponent($c3);
5
Als nächstes übergeben wir den Komponenten konkrete Wertepaare. Wir wählen dabei für alle Komponenten dieselben Wertepaare, um die spezifischen Unterschiede zu sehen.
1
2 $c1->AddPoint(-1, 5);
3 $c1->AddPoint(0, -2);
4 $c1->AddPoint(1, 9);
5 $c1->AddPoint(2, -4);
6
7 $c2->AddPoint(-1, 5);
8 $c2->AddPoint(0, -2);
9 $c2->AddPoint(1, 9);
10 $c2->AddPoint(2, -4);
11
12 $c3->AddPoint(-1, 5);
13 $c3->AddPoint(0, -2);
14 $c3->AddPoint(1, 9);
15 $c3->AddPoint(2, -4);
16
Bemerkung
-
Ob die Komponenten $c1, $c2 und $c3 erst an die Zeichenebene gebunden und dann die Wertepaare hinzugefügt werden oder umgekehrt, spielt keine Rolle.
Abschließend wollen wir den Container mit allen darin enthaltenen Komponenten noch zeichnen. Die Funktion Draw liefert uns den Bildkontext, den wir entweder lokal speichern, oder über ein Netzwerk versenden können. Als Argument sind Achsen- und Hintergrundfarbe, Breite und Höhe, sowie die Anzahl der äquidistanten Intervalle auf der X- bzw. Y-Achse anzugeben. Letztere Angaben dienen ausschließlich der Achsenbeschriftung, d.h. das Programm errechnet aus diesen, sowie dem minimalen und maximalen X- bzw. Y-Wert die entsprechende Beschriftung.
1
2 $image = $g->Draw(0x000000, 0xFFFFCF, 500, 250, 3, 7);
3 header("Content-type: image/gif");
4 imagegif($image);
5
Als Ausgabe erhalten wir:
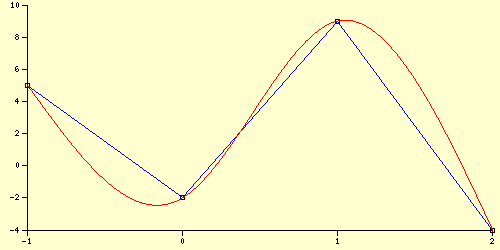
Es können anschließend problemlos weitere Wertepaare und/oder auch weitere Komponenten nachgetragen, und das Diagramm erneut gezeichnet werden. Wir ergänzen
1
2 $c4 = new GraphNaturalSpline(0xFF0000);
3 $g->AddComponent($c4);
4 $c4->AddPoint(0, 10);
5 $c4->AddPoint(1, 15);
6 $c4->AddPoint(2, 10);
7 $c4->AddPoint(3, -1);
8
9 $c5 = new GraphPoints(0x000000);
10 $g->AddComponent($c5);
11 $c5->AddPoint(0, 10);
12 $c5->AddPoint(1, 15);
13 $c5->AddPoint(2, 10);
14 $c5->AddPoint(3, -1);
15
16 $image = $g->Draw(0x000000, 0xFFFFCF, 500, 250, 4, 19);
17 header("Content-type: image/gif");
18 imagegif($image);
19
und erhalten mit den angepassten Werten 4 und 19 für die Anzahl der äquidistanten Intervalle auf den Koordinatenachsen:
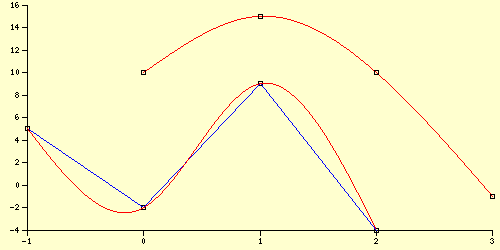
Beispiel 2 (Achsenformatierung)
-
In vielen Fällen wünschen wir eine spezielle Formatierung der Achsenbeschriftungen, so z.B. Zeit- oder Währungsangaben. Dazu müssen wir die numerischen Werte so wählen, dass wir daraus andere Darstellungen berechnen können. Um den formalen Overhead gering zu halten, verzichten wir auf spezielle Typvereinbarungen, und nutzen die formalen Möglichkeiten der Sprache gezielt aus. Wir geben eine Funktion an, die wahlweise auf die numerischen X- bzw. Y-Werte angewendet wird. In der funktionalen Programmierung sprechen wir vom sog. Mapping. Wir definieren für unseren Fall zwei Beispielfunktionen.
1
2 function ToCurrency($item)
3 {
4 return number_format($item * 100, 2, 0);
5 }
6 function ToDate($item)
7 {
8 return date("d.m.Y", time() + $item * 86400);
9 }
10
Können wir keine Berechnungsvorschrift angeben, dann können wir auch die in Frage kommenden Werte auf frei wählbare Werte, z.B. durch ein assoziatives Array, projizieren. Abschließend veranlassen wir noch die (erneute) Zeichnung. Dabei geben wir jeweiligen Funktionsnamen zur Formatierung der X- bzw. Y-Achse als ergänzende Parameter von Draw an.
1
2 $image = $g->Draw(0x000000, 0xFFFFCF, 500, 250, 3, 7, "ToDate", "ToCurrency");
3 header("Content-type: image/gif");
4 imagegif($image);
5
Als Ausgabe erhalten wir:
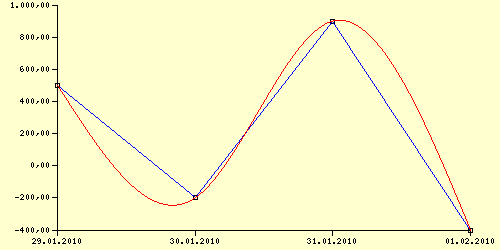
Beispiel 3 (Datenbankauswertung)
-
In vielen Webanwendungen wollen wir gerade die Daten aus einer Datenbank grafisch visualisieren. In diesem Beispiel wollen wie eine Gehaltskurve von Mitarbeitern zeichnen. Dazu benötigen wir zunächst eine geeignete Datentabelle.
| Id | Name | Gehalt |
| 1 | Martin A. | 3.230,00 |
| 2 | Theresa B. | 3.032,00 |
| 3 | Andrea C. | 1.897,00 |
| 4 | Günter D. | 2.980,00 |
Wie gehabt generieren wir wieder unseren Graphen in üblicher Form.
1
2 $g = new Graph();
3 $c1 = new GraphNaturalSpline(0xFF0000);
4 $c2 = new GraphPoints(0x000000);
5 $g->AddComponent($c1);
6 $g->AddComponent($c2);
7
Die Werte lesen wir über eine entsprechende mySQL-Anweisung aus der obigen Datentabelle aus. Mehr zum Thema mySQL findet man unter http://www.php-resource.de/tutorials/tutorial,27 oder http://www.php-resource.de/tutorials/tutorial,44. Wir probieren zunächst einen offensichtlichen Ansatz:
Zuerst überlegen wir uns, wie wir unsere Map-Funktion so definieren, dass wir auf der X-Achse die Namen der jeweilgen Mitarbeiter zu stehen haben. Wir müssen also von einer Zahl auf den zugehörigen Namen eindeutig schließen können. Es bietet sich dabei die Assoziation zwischen der Id-Nummer und dem zugehörigen Namen an.
1
2 function ToEmployer($item)
3 {
4 $result = mysql_query("SELECT Name
5 FROM mitarbeiter
6 WHERE Id = $item");
7
8 return mysql_result($result, 0, 0);
9 }
10
Sodann lesen wir die Werte aus der Datentabelle mit
1
2 $result = mysql_query("SELECT Id, Name, Gehalt
3 FROM mitarbeiter");
4 for ($i = 0; $row = mysql_fetch_array($result); $i++)
5 {
6 $c1->AddPoint((int)$row[0], (int)$row[2]);
7 $c2->AddPoint((int)$row[0], (int)$row[2]);
8 }
9
aus und erhalten mit
1
2 $image = $g->Draw(0x000000, 0xFFFFCF, 500, 250, 3, 5, "ToEmployer", "ToCurrency");
3 header("Content-type: image/gif");
4 imagegif($image);
5

Wenn Sie nun eine spezielle Sortierung z.B. ORDER BY Gehalt ASC fordern, dann hätte dies keine Auswirkungen auf die grafische Ausgabe. Das liegt daran, dass der Spline seinen Kurvenzug unabhängig von der Einfügereihenfolge der Knotenpunkte zeichnet. Achten Sie stets darauf, dass jede mathematische Funktion strikt von links nach rechts gezeichnet wird. Insbesondere werden alle Punkte stets nach ihrem X-Wert aufsteigend sortiert, bevor diese zur Brechnung herangezogen werden. Wir können also nicht mit der Id aus der Datentabelle als X-Wert sinnvoll arbeiten, und müssen daher eine eigene Id und zugehörige Assoziation zu Name auf Programmebene erzeugen. Wir projizieren also eine Zahl entsprechend der Rangfolge auf den zugehörigen Mitarbeiternamen.
1
2 $result = mysql_query("SELECT Id, Name, Gehalt
3 FROM mitarbeiter2
4 ORDER BY Gehalt ASC");
5
6 for ($i = 0; $row = mysql_fetch_array($result); $i++)
7 {
8 $mitarbeiter[$i] = $row[1];
9 $c1->AddPoint($i, (int)$row[2]);
10 $c2->AddPoint($i, (int)$row[2]);
11 }
12
13 function ToEmployer($item)
14 {
15 global $mitarbeiter;
16 return $mitarbeiter[$item];
17 }
18
Nun wird jede gewünschte Sortierung «richtig» gezeichnet.
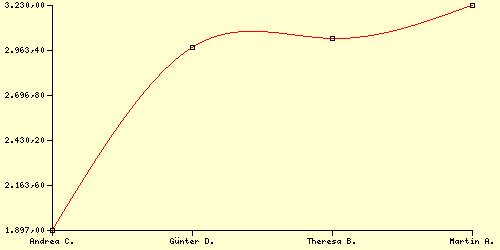
Beispiel 4 (Polygonzüge)
-
Die Komponenten vom Typ GraphLinear sind im Grunde als ein Streckenzug durch die zu interpolierenden Wertepaare gemäß ihrer Einfügereihenfolge zu sehen. Die lineare Interpolation ist also ein Spezialfall eines solchen Streckenzugs mit zusätzlich mathematischen Eigenschaften. Wir wollen uns folgend Polygonzüge ansehen.
1
2 # Zeichenebene
3 $g = new Graph();
4
5 # Komponenten
6 $c1 = new GraphLinear(0x0000FF);
7 $c2 = new GraphLinear(0xFF0000);
8
9 # Komponenten binden
10 $g->AddComponent($c1);
11 $g->AddComponent($c2);
12
13 # Werte hinzufügen
14 $c1->AddPoint(0, 2);
15 $c1->AddPoint(1, 2);
16 $c1->AddPoint(2, 3);
17 $c1->AddPoint(2, 4);
18 $c1->AddPoint(1, 5);
19 $c1->AddPoint(0, 5);
20 $c1->AddPoint(-1, 4);
21 $c1->AddPoint(-1, 3);
22 $c1->AddPoint(0, 2);
23
24 $c2->AddPoint(0, 2);
25 $c2->AddPoint(0, 1);
26 $c2->AddPoint(-1, 0);
27 $c2->AddPoint(-2, 0);
28 $c2->AddPoint(-3, 1);
29 $c2->AddPoint(-3, 2);
30 $c2->AddPoint(-2, 3);
31 $c2->AddPoint(-1, 3);
32
33 # Ausgabe
34 $image = $g->Draw(0x000000, 0xFFFFCF, 500, 250, 5, 5);
35 header("Content-type: image/gif");
36 imagegif($image);
37
Wir erhalten:
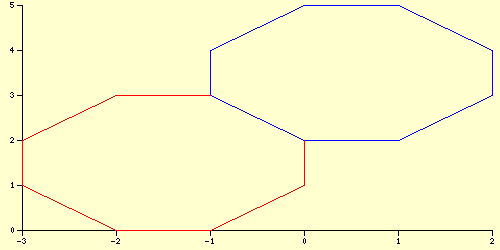
Der Sinn von Streckenzügen zeigt sich bei praktischen Vorgängen, die einen senkrechten Anstieg zur Folge haben. Dies können z.B. abrupte Gehalts- oder Auszahlungsänderungen sein. Wir betrachten ein Beispiel.
1
2 include ("graph.php");
3
4 # Zeichenebene
5 $g = new Graph();
6
7 # Komponenten
8 $c1 = new GraphLinear(0x0000FF);
9 $c2 = new GraphLinear(0xFF0000);
10
11 # Komponenten binden
12 $g->AddComponent($c1);
13 $g->AddComponent($c2);
14
15 # Werte hinzufügen
16 $c1->AddPoint(0, 4);
17 $c1->AddPoint(1, 4);
18 $c1->AddPoint(1, 3);
19 $c1->AddPoint(2, 3);
20 $c1->AddPoint(2, 4);
21 $c1->AddPoint(2.5, 4);
22 $c1->AddPoint(2.5, -2);
23 $c1->AddPoint(3.5, -2);
24 $c1->AddPoint(3.5, 6);
25
26 $c2->AddPoint(-1, 0);
27 $c2->AddPoint(-1, 2);
28 $c2->AddPoint(0, 2);
29 $c2->AddPoint(0, 0);
30 $c2->AddPoint(1, 0);
31 $c2->AddPoint(1, 2);
32 $c2->AddPoint(2, 2);
33 $c2->AddPoint(2, 0);
34 $c2->AddPoint(3, 0);
35 $c2->AddPoint(3, 2);
36 $c2->AddPoint(4, 2);
37 $c2->AddPoint(4, 0);
38
39 # Ausgabe
40 $image = $g->Draw(0x000000, 0xFFFFCF, 500, 250, 5, 4, "ToDate", "ToCurrency");
41 header("Content-type: image/gif");
42 imagegif($image);
43
Wir erhalten:
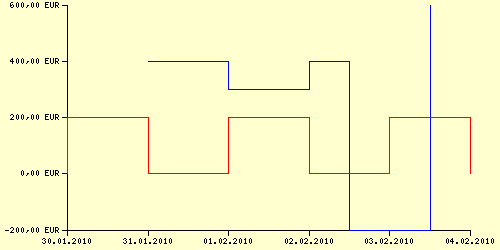
Erfahrungen
Hier Kannst Du einen Kommentar verfassen
Verwandte Beiträge
ASCII Datenbanken
ASCII Datenbanken sind eigentlich nur Textdateien, in denen man Daten speichert, die durch ein Trennzeichen voneinander getrennt sind. Dieses Tutorial zeigt wie es geht. Mit Übung und Lösung ...

Autor :
deep_space_nine@
Kategorie:
PHP-Tutorials
Thumbnails mit PHP erzeugen
Manchmal möchte man Bilder, die auf einer Website dargestellt werden sollen, verkleinern. Solche verkleinerten Bilder nennt man Thumbnails. ...

Autor :
Wolfgang13
Kategorie:
PHP-Tutorials
Objektorientiertes Programmieren
Dieses Tutorial beschreibt sehr gut die Wirkunsweise von objektorientiertes Programmieren. Also bestens geeignet um das objektorientierte Programmieren zu verstehen. ...

Autor :
phpsven
Kategorie:
PHP-Tutorials
Datenbankinhalt für Suchmaschinen aufbereiten
Sie haben eine Datenbankanwendung geschrieben und keiner weiß, welche Daten bei Ihnen zu finden sind. Suchmaschinen gehen natürlich nicht so weit, daß sie Abfragen an die Datenbank senden. Somit bleibt der Inhalt Ihrer Tabelle für Suchmaschinen unsichtbar ...

Autor :
Wolfgang13
Kategorie:
SEO Tutorials
Verschlüsslung bzw. Codierung von HTML Code in ASCII
HTML Code können wir ebenso gut in ASCII Code umwandeln. Zunächst einmal ein paar Sätze dazu, wozu man ASCII Zeichen benötigt und wozu Ihnen dieses Script dient. ...

Autor :
Lukas Beck
Kategorie:
PHP-Tutorials
Templates in PHP
Ein kleines Tutorial zum Einsatz von Templates in PHP am Beispiel der Apolda Templateklasse (kuerbis.org/template/) ...

Autor :
stulgies@
Kategorie:
PHP-Tutorials






