MySQL Tutorial: Das 'Nested Sets' Modell - Bäume mit SQL

Dieses Tutorial beschreibt die 'Nested Sets'-Technik, mit der man solche Bäume mit SQL performant konstruieren kann.

|23.02.2011 | gorski@ | 49647 | KAT : MySQL | | 2

2

4

Das visuelle Modell

Um einen Baum in einer SQL-Datenbank darstellen zu können, bieten sich sog. "Nested Sets" - verschachtelte Mengen - an. Für das Auslesen einer beliebig tiefen Baumstruktur benötigt man dann nur einen einzigen Datenbank-Query.

Hat man eine Oracle-Datenbank zur Hand, so ist es unnötig auf die hier beschriebene Methode auszuweichen, da Oracle den SQL-Befehl CONNECT BY (PRIOR) beherrscht, und sich somit leicht verkettete Datensätze samt ihrem Grad (Einrückungstiefe, LEVEL) herauslesen lassen. Mehr zu CONNECT BY findet sich in der freundlichen Oracle-Dokumentation.

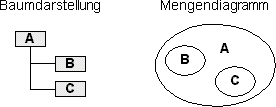
Ein Baumast mit zwei Blättern läßt sich als Menge folgendermaßen abbilden:

Mengen (Blätter) B und C sind Untermengen der Menge A, also Kinder der Wurzel A. In unseren Beispielen verwenden wir einfachheitshalber nur binäre Bäume - also Bäume mit nur jeweils höchstens zwei Kindern. Selbstverständlich ist die Technik auch auf allgemeine Bäume, deren Knoten wiederum beliebig viele Kind-Knoten enthalten können, anwendbar.

Was hier im Modell offensichtlich ist, muß in einer Datenbanktabelle nicht nur als solches gekennzeichnet werden, es muß auch die Reihenfolge (B vor C) gespeichert werden.

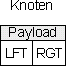
Für diese Speicherung der Abhängigkeit innerhalb einer solchen Struktur benötigen wir zwei Tabellenfelder (im Folgenden LFT und RGT gennant). Die Payload, also die Nutzlast des Knotens beschränkt sich in unseren Beispielen zunächst nur auf einen Buchstaben (A .. n), um die verschiedenen Knoten des Baumes benennen zu können.

Dies sei ein Beispielknoten mit der Nutzlast und dem Zahlenpaar, das die Abhängigkeiten repräsentiert:

Um die Reihenfolge der Knoten zu sichern, speichern wir in den LFT- und RGT-Feldern Zahlen, die uns beim Herauslesen der Daten ermöglichen, mit dem den sog. Preorder-Walk den Baum zu traversieren (zu durchlaufen) - beim Preorder-Walk bedeutet das, dass zuerst der Wurzel-Knoten, dann alle Knoten, die "links" vom jeweiligen Vaterknoten, danach alle Knoten die "rechts" davon liegen, gelesen werden.

Die LFT- und RGT-Zahlenpaare setzen sich für unseren kleinen Beispielbaum folgendermaßen zusammen:

Das Verständnis für die LFT- und RGT-Zahlen ist essentiell, um das Nested-Sets-Prinzip zu erfassen: von der ersten LFT-Zahl (die "1" im Wurzel-Knoten A) ausgehend, wird zuerst das linke Blatt (B) durchlaufen, danach das rechte (C). Bei dieser Traverse - einfach den Pfeilen folgen - wird jeweils eine Zählervariable um den Wert 1 inkrementiert, und zuerst im LFT- und dann nochmals inkremetiert im RGT-Feld gespeichert.

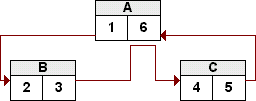
Das zweite Beispiel sieht damit nicht mehr so kompliziert aus:

Ausgehend von der Wurzel A wird wiederum jeweils der linke Teilbaum durchlaufen, dann jeweils der rechte. Die LFT- und RGT-Zahlen werden in der vorgebenen Reihenfolge inkrementiert. Besitzt ein Kind-Knoten seinerseits Kinder, so wiederholt sich die Prozedur ebenfalls für diesen Kind-Knoten etc.

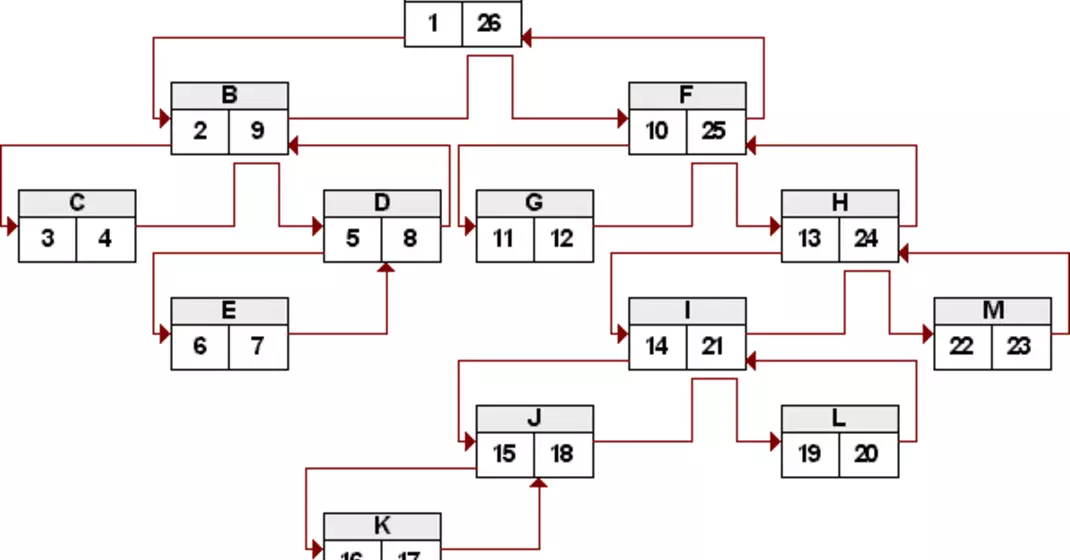
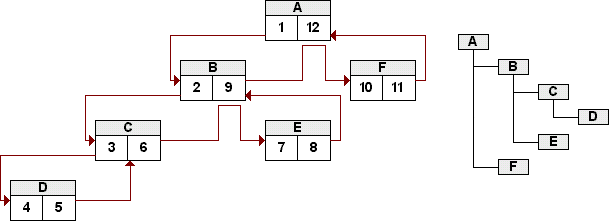
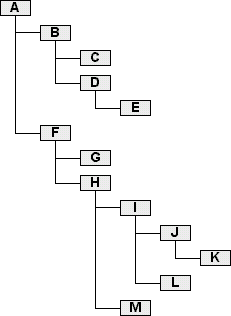
Die Reihenfolge des Preorder-Walks ist den Pfeilen oder einfach nur dem Gesetz des Alphabetes zu entnehmen. Dieser Nested Sets-Baum würde in einer seiner Nutzformen den Baum darstellen, der im rechten Teil der Grafik abgebildet ist.

Die Mengendarstellung dieses Baumes könnte folgendermaßen aussehen:

Aufgrund der verschiedenen Zahlenabhängigkeiten kann man sich leicht vorstellen, dass die Nested Sets-Technik sich primär für Strukturen eignet, die nur gelesen werden müssen, z.B. die Darstellung von Forumsbeiträgen oder Katalog- und Menübäumen, da bei jeder Änderung des Baumes alle Abhängigkeiten geändert werden müssen. Bei Forumsbeiträgen oder ähnlichen Bäumen kann man davon ausgehen, das in 95% der Fälle der Zugriff lesend erfolgt.

Bäume die sich öfters dynamisch verändern (müssen) - z.B. Sortierung - werden mit dieser Technik ausgebremst.

Zum hoffentlich besseren Verständnis der Nested Sets-Zahlen hier nochmal ein größeres Beispiel:

Wer sich diesen Baum genauer anschaut, dem werden mehrere Zusammenhänge der Zahlenpaare klar:

• Wurzel (LFT) = 1
• Wurzel (RGT) / 2 = Anzahl der Knoten im Baum
• Blatt (RGT) - Blatt (LFT) = 1
• Für alle Knoten außer der Wurzel gilt: (Knoten (RGT) - Knoten (LFT) - 1) / 2 = Anzahl der Kind-Knoten
• Alle LFT- und RGT-Werte sind eindeutig

Diese Abhängigkeiten sollte man sich einprägen, sie werden uns später von Vorteil sein.

Kommentare zum Tutorial Tutorial kommentieren Neuen Kommentar schreiben Benutzen Sie [code] und [php] um Codes, SQL-Queries oder php korrekt darzustellen!   25.02.2010 14:59:07 Schöne SQL-Erweiterung http://www.php-resource.de/forum/blogs/amicanoctis/25-nested-set-move-s ... 25.05.2009 15:47:58 Das 'Nested Sets' Modell verwenden wir häufig in unseren Projekten. Dieses Tutorial war gerade ... Alle Kommentare anzeigen ...